Límite. Diccionario de términos lacanianos
Tweet
Dada una sucesión {xn}, se dice que x es el límite de {xn} cuando, intuitivamente, a valores mayores de n corresponden valores de xn cada vez más cercanos a x. Cuando x es un número, ésto significa que la distancia entre xn y x tiende a cero cuando n tiende a infinito.
Pero también puede pensarse que x es infinito: en ese caso se dice que la sucesión {xn} tiende a infinito o diverge, cuando el valor de xn (o bien: su distancia al origen) crece indefinidamente.
En el caso de una función, se dice que L es el límite de f cuando x tiende a a, y se escribe:
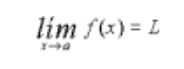
cuando, intuitivamente, para valores de x cada vez más cercanos al valor a, el valor de f(x) resulta cada vez más cercano a L. Si el valor de L coincide con el de f(a), f es una función continua en a. Nuevamente, tiene sentido considerar el caso L = ¥ , o incluso a = ¥ .
Volver al índice «Letra L«
Volver a listado de «diccionario de términos lacanianos«

